Inverse Matrices
At this point, you may be wondering why the Fourth Horseman of the Math Apocalypse, division, seems to be getting overlooked. Well, the fact is that you can't do division with matrices. That's okay, though, because if you can't divide by x, for example, you can multiply by its inverse:
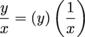
The same is true with matrices. All we need to know is how to find the inverse, right?
Check this out in the context of solving an equation:
2x = 4
Normally, we would just divide each side by 2 in order to solve this:
2x = 4

x = 2
But what if we can't divide? Think of it this way. Dividing by 2 in this example is the same as multiplying by the inverse of 2:
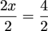 is the same as
is the same as 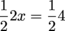 because
because  is the inverse of 2.
is the inverse of 2.
Let's think this through with all variables.
If this is our equation:
ab = c
...and we need to solve for b without division, we need to find the inverse of a and multiply both sides by that:
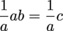
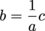
No division in sight. Ready to do this with matrices? Super important note before we get started: we're only gonna worry about finding the inverses of 2 × 2 matrices right now. It gets a bit more hairy with matrices bigger than 2 × 2, so we'll save that for Pre-calculus.
With regular numbers, we could multiply any number by its inverse and get 1. Right? Like this:
2 ×  = 1
= 1
It's the same deal with matrices. When we multiply a square matrix by its inverse, we should get an identity matrix as our product (since the identity matrix is the matrix version of the number 1).
Let's say we want to find the inverse of this matrix:

To do that, we bring back our old buddy, the determinant. Remember him? First we find the determinant. Our determinant in this case would be:
ad – bc
Crisscross minus applesauce. Then we throw that number into the denominator of a fraction. Multiply that fraction by a twisted-up version of the original matrix where we swap a and d (the upper-left and lower-right entries) and swap the plus/minus signs on b and c. Talk is cheap, though, so here's the formula for finding the inverse of the above matrix:
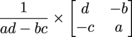
Boom, there's our inverse. That fraction at the front is 1 over the determinant, and the rest is just pluggin' and chuggin'.