From classics like Die Hard and Terminator to the legendary Kung Pow: Enter the Fist, action movies have provided countless hours of bated breath, wide-eyed stares, and unrealistic maneuvers that later become the subject of MythBusters episodes. (Ever wondered if it's actually possible to outfox a laser beam alarm system? Find out!) What beats a bucket of buttery popcorn and all the hand-to-hand combat, ginormous explosions, and obligatory car chase scenes that only action movies can provide?

Well, geometry doesn't have car chase scenes per se, but head-on crashes are far more common than you might think. You never expected math to be this action-packed, did you?
In geometry, we call two lines that crash into each other perpendicular, which is kind of the opposite of parallel. Not only do perpendicular lines intersect, they really, really intersect. We're talking a full-on crash that makes not one, not two, not even three, but four right angles.
Perpendicular lines make four right angles? Proving it is elementary, my dear Watson.
Sample Problem
Given: Lines m and n are perpendicular.
Prove: ∠1, ∠2, ∠3, and ∠4 are right angles.
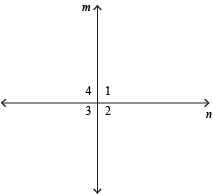
| Statements | Reasons |
| 1. Lines m and n are perpendicular | Given |
| 2. ∠1 is a right angle | Definition of perpendicular |
| 3. m∠1 = 90 | Definition of right angle |
| 4. ∠1 ≅ ∠3 | Vertical angles theorem |
| 5. m∠3 = 90 | Definition of congruent angles, substitution |
| 6. ∠1 and ∠4 are supplementary | Given in figure, straight angle theorem |
| 7. m∠1 + m∠4 = 180 | Definition of supplementary angles |
| 8. m∠4 = 90 | Substitution of (3) into (7) |
| 9. ∠4 ≅ ∠2 | Vertical angles theorem |
| 10. m∠2 = 90 | Definition of congruent angles, substitution |
| 11. ∠1, ∠2, ∠3, and ∠4 are right angles | Definition of right angle using (3), (5), (8), and (10) |
So when two perpendicular lines intersect, we got something that looks like this.
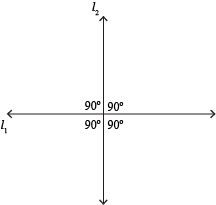
Marking every angle with a 90° or right angle box is a little redundant though, so we usually just mark one of them. That's enough to know the rest of them are right angles, too.
Parallel lines get their own symbol, so it only makes sense that perpendicular lines get their own symbol too. We denote that lines FR and ED are perpendicular by writing FR ⊥ ED.
Perpendicular segments also have the peculiar quality of being the shortest distances from any point to another line. So if you're standing 20 feet away from a wall, that measurement is along a segment that's perpendicular to the wall.
It's also important to know that if two lines are both perpendicular to a third line, then those two lines are parallel to each other. So if lines f and g both intersect line b at 90° angles, then f and g are parallel. You can use your knowledge of corresponding angles, alternate interior angles, or alternate exterior angles to prove this.
Also, make sure you know that orthogonal means the same thing as perpendicular. Some teachers or textbooks like to use it because it makes them sound really fancy, like using the word "loquacious" instead of "talkative." They can use all the five-dollar words they want. We'll stick to ones that only cost a buck fifty and get a side of fries with the extra change.