First we take the derivative. 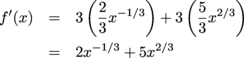
By some mildly tricky rewriting, we can factor this formula. 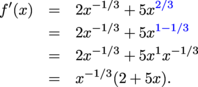
Now that the derivative is nicely factored, we'll do the rest of the job. f ' is undefined when x = 0, since 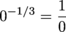
is undefined. Since f (0) is defined at 0, x = 0 is a critical point. Finally we want to find the roots of the derivative. We have f '(x) = x-1/3(2 + 5x). The factor x-1/3 is never 0. The factor (2 + 5x) is 0 when  , so we've found another critical point. , so we've found another critical point. The final answer: there are critical points at x = 0 and at  . . If we zoom in enough on the graph, this makes sense. The derivative doesn't exist at 0, and there appears to be a horizontal tangent line at  : : 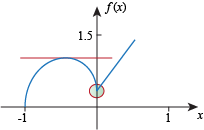
| 

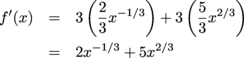
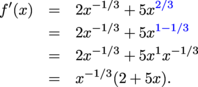
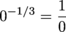
 , so we've found another critical point.
, so we've found another critical point.

