Be Careful: There are two ways to use substitution to evaluate definite integrals. When evaluating a definite integral, make sure you know which way you're using them.
Way 1: First integrate the indefinite integral by substitution.
We know how to use substitution to find indefinite integrals. This means we know how to use substitution to find antiderivatives.
To use substitution to find an antiderivative, we first use substitution to find the indefinite integral. Then we drop the + C, which is the same thing as setting C = 0. The indefinite integral is an infinite family of antiderivatives, and setting C = 0 gets us one antiderivative out of that infinite family.
Way 2: Change the variables, and never go back.
The other way to evaluate definite integrals by substitution is to change the variable of integration and also change the limits of integration to match the new variable. With this method, we never have to put the original variable back in.
Here are the two steps to follow when integrating a definite integral via Way 2:
- Do the substitution in the definite integral, remembering to change the limits of integration.
- Use the FTC to integrate the resulting definite integral.
Going back to definite integrals, the Fundamental Theorem of Calculus says that we can evaluate the definite integral

by finding an antiderivative F of f and taking the difference
F (b) – F (a)
which is abbreviated by
 .
.
So long as we can use substitution on the integrand, we can use substitution to evaluate the definite integral.
There are two steps:
1. Use integration by substitution to find the corresponding indefinite integral. This gets us an antiderivative of the integrand.
2. Use the FTC, with the antiderivative from (1), to find the definite integral.
Remember, first you do substitution to get a new definite integral, with a new variable of integration and new limits of integration. Then you evaluate the new definite integral using the FTC.
Way 1 or Way 2? Help!
There are two obvious questions that might be bouncing around in your head right now.
- "Should I use Way 1 or Way 2?"
- "How do I know when to use Way 1 and when to use Way 2?"
There's good news and bad news...no, actually there's just good news. Either way will work. As long as you know which way you're using and do it correctly, you'll get the right answer. To test this, work out these integrals using Way 2 and work out these integrals using Way 1. You should get the same answers you got before. So the easiest answer to both questions is "Use whichever way you like better."
It's true that some definite integrals may be shorter with one way than with the other. The best way to figure out when one way is shorter than the other is to do a bunch of practice problems.
Example 1
Find an antiderivative of 3(3x + 1)5. |
Example 2
Evaluate |
Example 3
Evaluate |
Example 4
Use Way 2 to evaluate
|
Exercise 1
A test contained the following question:

Laurie wrote down the following answer:
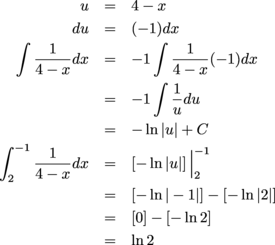
What did Laurie do wrong? What is the correct value of the integral?
Exercise 2
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Exercise 3
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Exercise 4
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Exercise 5
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Exercise 6
Evaluate the definite integral using Way 1(first integrate the indefinite integral, then use the FTC).

Exercise 7
A test contained the following question:

KT wrote down the following answer:

What did KT do wrong? What is the correct value of the integral?
Exercise 8
Evaluate the definite integral by substitution, using Way 2.

Exercise 9
Evaluate the definite integral by substitution, using Way 2.

Exercise 10
Evaluate the definite integral by substitution, using Way 2.

Exercise 11
Evaluate the definite integral by substitution, using Way 2.

Exercise 12
Evaluate the definite integral by substitution, using Way 2.



 .
.
 is an antiderivative of 3(3x + 1)5.
is an antiderivative of 3(3x + 1)5.
 .
. .
. .
.
 .
.













 .
.




 . So
. So






















 we have
we have







