In the Real World
Logs are everywhere. Birch logs, mahogany logs, pine logs—okay, we'll stop there.
Our original statement still holds true. Logs are everywhere, and so are exponents. Most anything that starts slow and then increases really fast can be modeled using an exponential function, and similarly things that start quickly and then slow down in a hurry (oxymoron?) can often be modeled using a log function.
Bacterial Growth
Let's start with something really yummy: bacteria.
Get that funny look off your face. There are bacteria all around you: on the table, the bed, your pillow, inside of you.
Those little buggers like to multiply like there's no tomorrow, through a process known as binary fission. No, not nuclear fission. That'd be a little scary. By fission, we mean "splitting."
If every bacterium splits into two, and those two bacteria split into two each, and so on, we've got an exponential function on our hands (Lucky us, right?)
Sample Problem
What exponential function f (x)= Cbx would model bacteria growth per second, assuming the bacteria split every 4 seconds and we start with 20 bacteria? In this case, we'll simplify any irrational numbers to four decimal places.
In the beginning of time, x = 0, there's 20 bacteria. That means f (0) = 20, so we can plug in 20 for f (x) and 0 for x.
20 = Cb0
20 = C
At 4 seconds, x = 4, the bacteria doubles, so f (4)= 40.
40 = 20b4
2 = b4
b ≈ 1.1892
Then put it all together like a puzzle:
f (x) = 20(1.1892)x
Sound
What happens when you're at a loud rock concert? Your hair stands up, your brain hides in the corner of your skull, and your skin ripples in waves. Compared to a normal conversation, the sound at this concert is about 100,000 times more intense. We can measure this intensity on the decibel scale, which is a logarithmic scale.
The decibel scale begins at 0, which is a "reference level" of sound intensity that humans can just barely hear. For every increase of the decibel level by 10, the sound intensity increases by 10 times the previous intensity. Sound intensity isn't quite the same thing as volume, though, but that's math for a rainy day.
Moore's Law
A smartphone today is more powerful than the most powerful, room-filling supercomputers just a few decades ago. This is thanks to the collective efforts of thousands of smart people all around the world. The cool thing about computers is that as they get better, they help us make better computers, which yields better computers, which helps…well, you get the idea.
The number of transistors on a single computer processor chip, which is a rough estimate of how powerful it is, doubles about every 18 months. This trend is known as "Moore's Law," named for the co-founder of computer supergiant Intel, Gordon Moore.
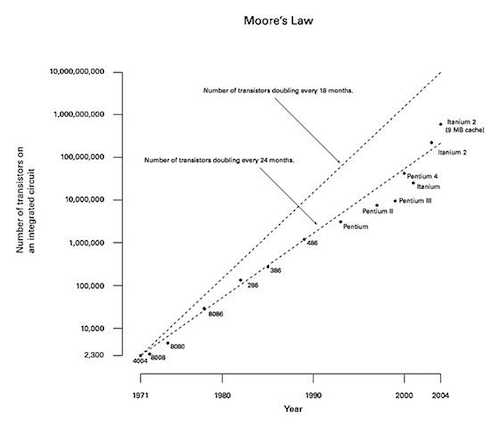
Notice how the y-axis of this plot looks all kinds of odd. That's because it's not following a linear trend anymore; every tick mark represents ten times the previous value. You could even think of it like this: 104, 105, 106, and so on, which is commonly used and known as "scientific notation." That y-axis is a good example of a logarithmic scale.
Sample Problem
Write out the exponential function f (x)= Cbx that would represent Moore's Law, assuming x is measured in years. Assume you start with 1 transistor when x = 0 years, and simplify any irrational numbers to three decimal places.
An easy way to solve this problem is to start with C. If there's one very lonely transistor on the chip to start off (f (0)= 1), then you can solve the following equation:
1 = Cb0
1 = C
Because 18 months equals 1.5 years, and you know that the number of transistors doubles every 18 months, you can then write:
b1.5 = 2
We can also write it like this:
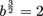
If we raise each side to the power of 
:
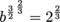
We get an irrational base of 1.58740…, which we can simplify to just 1.587. Now our final answer, for one million fake dollars, is:
f (x) = 1.587x
Essentially, this means that every year, the number of transistors increases by about 1.587 times! At this rate, in a few decades we won't even need brains anymore. Or hands.
Compound Interest
Remember that funny lil' number, e? It's time to pull up the curtains on one of its many uses. Like we mentioned before, it's the sum of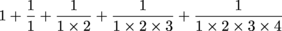 
, up to a gazillion-billion-billion. (Note: this is not a formal definition; do not use it in a term paper.)
A very common use of e is in calculating compound interest. When money accumulates interest, it could be "compound interest" that accumulates every year, quarter, month, week, day, or whichever unit of time fits your delicate taste. Continuously compounded interest takes accumulation to the next level, though—the hardest, fastest, most extreme accumulation there is. Every sliver of a second that makes up a day contributes to the generation of interest, and this can make quite a big difference in the long run.
The formula for continuously compounded interest is A = Pert, where A is the amount of money in our account after t years, P is our starting amount, and r is the interest rate.
Sample Problem
If you have $100 in your bank account, which has a continuously compounded interest rate of 9.5% (lucky you), how many years will it take for it to grow to $150? Simplify to two decimal places.
Let's bust out our new formula, A = Pert. The original investment is $100, and we need to get $150. That means A = 150 and P = 100. Our interest rate is 9.5%, so we convert that to a decimal to get r = 0.095. Now we can write out:
150 = 100e0.095t
To solve for t, first divide the coefficients:
1.5 = e0.095t
Then take the natural log of both sides and solve:
ln 1.5 = ln e0.095t
0.405 = 0.095t ln e
0.405 = 0.095t
t ≈ 4.26 years
We're rich. Uber rich. Well, we'll be 50% more rich in four years and change. Not too shabby, but we'd better start saving more. That money isn't going to grow on trees.