Triangle Proportionality Theorem

Similar triangles can be located any number of places, including one inside the other. And if you're working with a big problem, there may be a third similar triangle inside of the first two. And technically there could be a fourth one, even smaller, inside of the third.

But before Leonardo DiCaprio or Joseph Gordon-Levitt show up and draw us into a ridiculous triangle-ception situation, let's just state for the record that we're only going to deal with the first two, which are actually created by taking one triangle and shooting a line through it. Because if that line is parallel to one side of the triangle, it'll create two similar triangles.

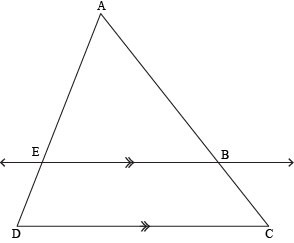
Here, ∆ACD ~ ∆ABE. We'll prove this a little later. For now, we're going to focus on the chopped-up side pieces.

In this illustration, line EB is parallel to side DC. We can see that it intersects sides AC and AD. This creates proportional segments:

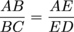
In fact, we even have a theorem about this: the Triangle Proportionality Theorem. Apparently, mathematicians got quite a giggle when they first came up with it, since it's earned the nickname "The Side-Splitter Theorem." To be honest, we don't really get it. It must be an inside joke.

The Triangle Proportionality Theorem says that if a line is parallel to one side of a triangle, then it splits the other two sides into proportional sections.

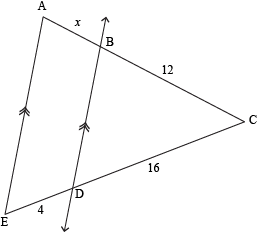
We can use this theorem to find the value of x in ∆ACE. We're given that line BD is parallel to side AE, and three of the resulting segment lengths are also given. To find the missing piece, set up a proportion comparing the side lengths:

¹⁶⁄₄ = ¹²⁄_x

Now cross-multiply and solve for x:

16x = 48
x = 3

Or, the quick way would be to notice that ¹⁶⁄₄ = 4, so ¹²⁄_x must also equal 4, which would also give us x = 3.

Sample Problem

Find the value of y.

We'll solve this one with a proportion. The TPT says we can.

Cross-multiply to get 3y = 10. Divide both sides by 3 get y = 3.3.

You may have recognized the TPT as a classic If-Then conditional statement. And this time, the converse is true: if a line splits two sides of a triangle into proportional sections, then the line is parallel to the third side.

Since , we know that MP || NO.

We're kind of on a roll here with the conditional statements, so let's keep going with the contrapositive of the TPT: if the side segments aren't proportional, then the line that created them isn't parallel to the third side. True?

Of course, true! (If the statement is true, then the contrapositive is also full of truthiness.)

Here, , so WY is not parallel to VZ.

Sample Problem

State whether QS || PT.

If the segment lengths are proportional, then we know the line is parallel to the side. And, if they're not proportional, the line isn't parallel to the side. In this case, , so no, QS is not parallel to PT.