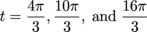We're kicking things up a notch. Now, there will be all kinds of expressions inside of the trig functions, not just t by itself. Do you think you can handle it? If not, take a break and come back to it tomorrow. We'll be here, we can wait.
Sample Problem
Solve sec (4t) = 2 on the interval [0, π].
The second-most important thing to know about this problem is that it doesn't matter how many t's are inside the trig function: they don't change the right-hand side of the equation. We have sec (something) = 2, and we solve it the same way as last time.

By checking the unit circle. Secant is the reciprocal of cosine (not sine! never sine!), so it will equal 2 when  or
or  (plus or minus 2π).
(plus or minus 2π).


Do not, do not, do not say that this stuff equals t. That's the most important thing to know about this problem. It is super easy to forget this; we did it ourselves when writing this problem, embarrassing as that is. Instead, our (something) should be 4t:


We now divide each side of these equations by 4, to get t by itself:


Yes, even 2πn gets divided. That's easy to forget, too. Don't do it, or the Ghost of Mathematics Future will show up and tell you how horribly you've mucked things up.
(By the way, is he someone that died in the future and traveled back in time to tell us about it, or someone who is a ghost now and can see the future? We just don't know.)
Anyway, now we plug in some values for n to find the other solutions within the interval. When n = 1:


 falls in the interval [0, π], but
falls in the interval [0, π], but  doesn't. Checking n = 2 gives
doesn't. Checking n = 2 gives  , which is also too big.
, which is also too big.
Going in the other direction, with n = -1, we have:


We add  to our stable of correct answers, while tossing
to our stable of correct answers, while tossing  aside. If we subtract another
aside. If we subtract another  out, we end up with another negative number, which means we've exhausted our supply of angles.
out, we end up with another negative number, which means we've exhausted our supply of angles.
That means our final answer is  . We keep getting the right answers, but Regis refuses to give us our million dollars.
. We keep getting the right answers, but Regis refuses to give us our million dollars.
Sample Problem
Solve sin (π – t) = cos (π – t)
We follow our standard procedure here. Isolate the trig function with t; find what (something) equals; find all the solutions; celebrate with fireworks.
However, we're seeing double here. There are two functions with t in them. In this case, we can fix this with a little division. Knowing that sine divided by cosine equals tangent, we just divide:

tan (π – t) = 1
That's better. It only worked, though, because the stuff inside each trig function, (π – t), was the same. If they weren't identical, we'd be out of luck.
To find where sine and cosine are equal (and so tangent will be 1), we check the unit circle.

Will the unit circle ever stop being so helpful? We hope not. The angles we want are π/4 and 5π/4; remember, tangent is positive in quadrants I and III.


There's a trick we can use before going any further that will make this problem a little easier.

Our two base solutions are on opposite sides of the circle, π away from each other in both directions. Instead of having two sets of solutions that repeat every 2π, we can have one set of solutions that repeat every π.

We can get the correct answer either way. It's like choosing between two different routes to your destination, where one route is shorter and has nicer weather.
Now we need to replace that (something) with (π – t), while keeping an eye on that negative sign.

If you were watching the signs, then you've already noticed that we didn't change it for πn. That's because n can be any integer, positive or negative, so it just absorbs the negative sign. It's kind of gross, really.
Anyway, we have our solutions. We can go back to the original problem and double check we did everything right. For instance, when  :
:

And now, we lie back in our easy chair and watch the boom.
Example 1
Solve |
Example 2
Solve (cos (3t))2 + 2(cos (3t)) + 1 = 0 on the interval [0, π]. |
Example 3
Solve |
 .
.
 are
are  and
and  .
.


 .
. . That means that
. That means that  . For this problem:
. For this problem:
 .
. .
.



 are π away from each other, so we could have consolidated our answer a bit. We don't have to, though; plug in a few values for n and be amazed as you get all of the same answers.
are π away from each other, so we could have consolidated our answer a bit. We don't have to, though; plug in a few values for n and be amazed as you get all of the same answers.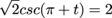






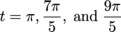

 the interval [0, 6π].
the interval [0, 6π].