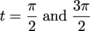What is an equation? A miserable little pile of secrets. At least, it can feel pretty miserable if you're stuck on an even-numbered problem for hours. Luckily, we here at Shmoop don't believe in withholding the answers from you.
A trigonometric equation works just like any other; we have a variable, an equal sign, and a request to find out where the two sides meet. The only difference is that our variable is holed up inside a trig function, refusing to come out.
Take, for instance,

We want to know every value of t that will make this equality true. We're nosy like that. We do that by getting (sin x) by itself, maybe ask it a few questions.

Now, what values of t result in sine having a value of  ?
?

Let's use the unit circle to find out. Sine is associated with the y-coordinate. Looking around the circle, we see that the angles  and
and  have positive
have positive  as their y values.
as their y values.
We're not done yet, though. Much like history, your rambling uncle, and a school assembly, the unit circle repeats itself.

If we add—or subtract—2π from an angle, we end up in the same spot on the unit circle, and that new angle will have the same co-ordinates. Thus, we have:


Where n = 0, ±1, ±2, …. There are an infinite number of angles that make  . We tried counting to infinity once, but stopped after 5. We got bored.
. We tried counting to infinity once, but stopped after 5. We got bored.
Sometimes, we only want some of the solutions for a trigonometric equation; those that fall within some interval.
Sample Problem
If a tree falls in the forest, and no one is around, how much wood could a woodchuck chuck from it?
No, wait, that's the wrong question.
Solve  within the interval -2π to 2π.
within the interval -2π to 2π.
Hey, we've mostly solved this problem already. Isn't that nice? It's much easier than that woodchuck problem, in any case.
All we need to do is take our solution from before, when we didn't specify any interval, and plug in some values for n.


When n = 0,

Both of these solutions are in-between ±2π, so we're good there. For n = +1:


And for n = -1:


 and
and  fall in the interval, but
fall in the interval, but  and
and  are out of bounds. Dumping them like a bag of sweaty socks at the laundromat, we have:
are out of bounds. Dumping them like a bag of sweaty socks at the laundromat, we have:

as our solutions. If we used n = ±2, we wouldn't find anything. Now if you'll excuse us, we have some laundry to do.
Example 1
Solve |
Example 2
Solve tan t = -1 on the interval [-2π, 2π]. |
Example 3
Solve |
 .
. .
.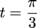
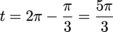
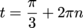
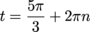
 angles.
angles.









 .
. on the interval
on the interval  .
.




 is
is  more than π, and
more than π, and  is
is  less than 2π.
less than 2π. , covers the left half of the unit circle, meaning the second and third quadrants. That means the only solution is:
, covers the left half of the unit circle, meaning the second and third quadrants. That means the only solution is:
 .
.

 .
.

 on the interval [2π, 4π].
on the interval [2π, 4π].
 .
. .
.