To misquote Tolstoy, "All good graph algorithms are alike; every bad graph algorithm is bad in its own way." Something like that.

Graph algorithms—the ones that go through graphs to find optimal paths—work for a pretty simple reason: the shortest path between any two places is a sum of all the shortest paths in-between those two places.

Wait, what?

If you're walking somewhere five feet away, you're going to try to take the path that's closest to a straight line. If you cut that line in half, it would no longer be one straight line, it'd be two, two and a half foot straight lines to the place you need to go. The distance is now the sum of those two lines.

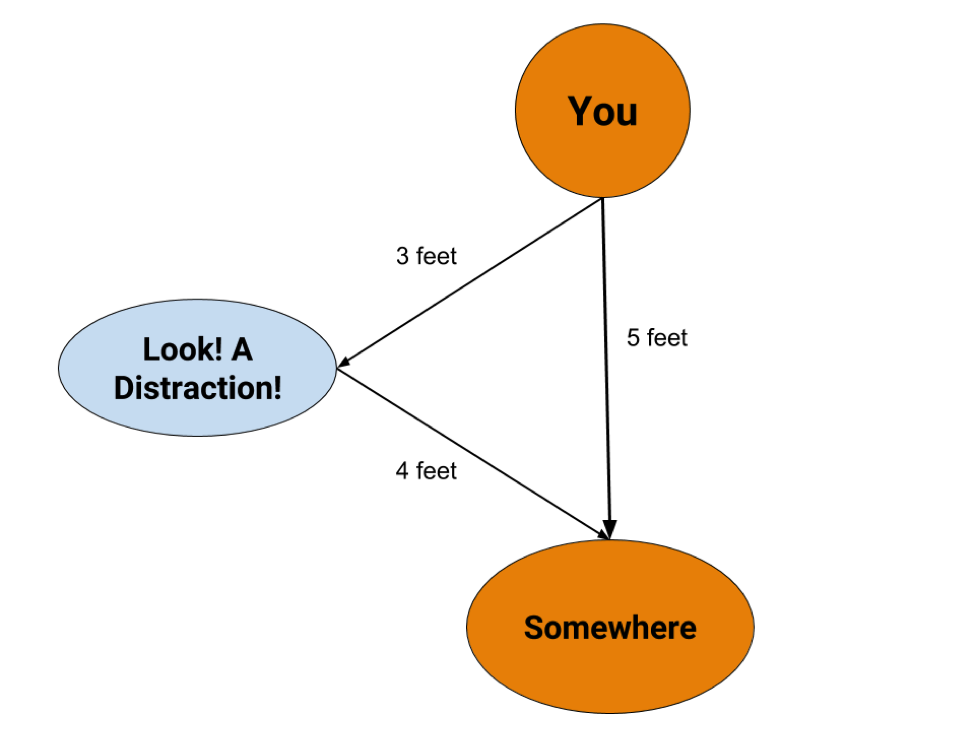
Instead, though, if you fell prey to a distraction on the side, even though you'd be going three feet to the distraction, you'd take another four feet to make it somewhere, making the distance traveled seven feet instead of five. You wouldn't be taking the sum of the shortest paths anymore because your line is no longer straight.

The same principle is true in graphs. If you've found the shortest path between two places, it's because you've found the series of shortest paths that all add up to the shortest path from one node to another.

Take a look at this graph:

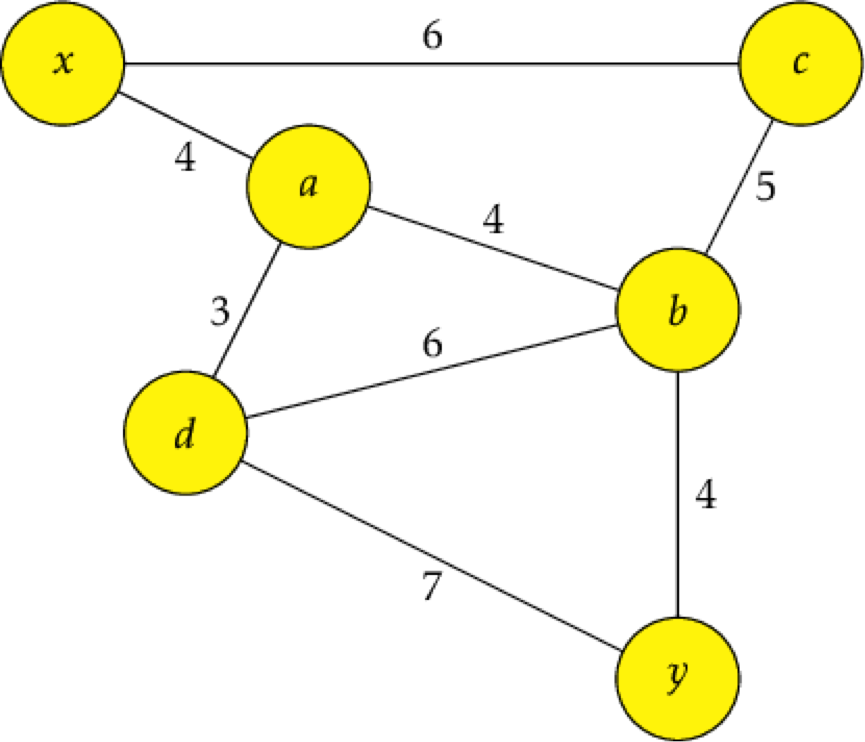
If we're trying to get from A to D, the shortest distance is going to be that straight line between them, which has a weight of three. But how about from X to D? There aren't any direct lines between them, but if we take the series of shortest paths to get there, we'll be able to find the shortest path total. If we go from X to A to D, that's going to be the shortest path if we're taking the shortest paths between X and A and the shortest paths between A and D. Otherwise it won't be the shortest path.

But these paths (and direction decisions) can be broken down even further.

We chose to go through A because it was X's closest, cheapest neighbor. If, instead, C was X’s cheapest neighbor at 2, then the algorithm would probably have gone there first instead, because that would currently be the cheapest way to get to D. If it kept going with Dijkstra's algorithm, though, the cost of going from C to B to D is still going to become greater than going through A.

Because we're prioritizing the nodes we check by whatever's the shortest distance, if we end up finding the final node in the path before checking every other node in the graph, we know that we've found the shortest path. Because it's coming up as the lowest cost in the list, no path that we could search for after processing the final node could give us a shorter path because they're starting with more of a cost than the ending node. So we know that a path like

X → C → B

can't possibly be a cheaper path to D because that path alone is more expensive than the path we've already found to D, much less the extra edges it would take to finally reach D.

Dijkstra’s algorithm is very thorough—J.R.R. Tolkien and all his writings about Middle Earth, including its histories/mythologies/languages/religions kind of thorough. It

• checks
• double-checks 
• triple-checks

the costs from every node to every other node (whether directly or indirectly) to make sure they're all taking the cheapest path.

Because the algorithm isn’t finished until the destination node is added to the visited list, all of its neighbors have to have been visited (and their costs minimized) beforehand, which means that all the neighbors' neighbors have to have been visited too, and the neighbors’ neighbors’ neighbors have to have been…well, you get the idea.

The cheapest route isn't always the most direct one, so it has to be thorough to catch all possibly cheapest scenarios. You can't trust each cheapest route to take you there, though, since you could end up taking a long, lolly-gagging route that actually adds to make a more expensive path than something that looks more expensive in the short run but is actually cheaper in the long run. Like the path between X and Y.

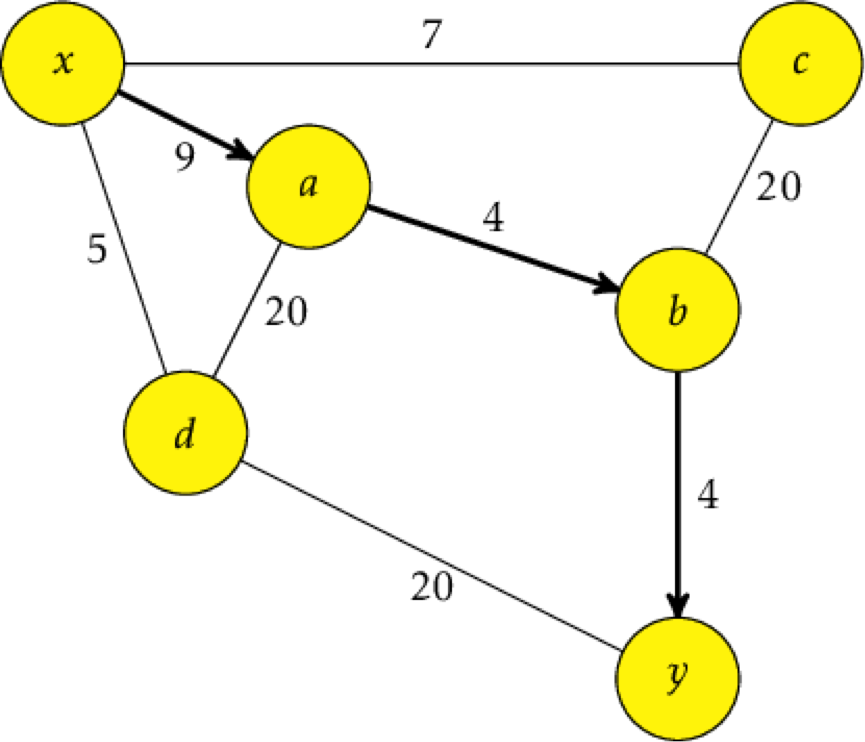
Because Dijkstra's focuses on the overall cost instead of the weight of each edge, going with the marginally cheaper path initially won't stop you from finding the actual cheapest total path because that cost keeps a running total of how much it's taking to get somewhere.

As soon as the cost gets too high, it's rejected for a cheaper path, ensuring that we'll always find the cheapest path from start to finish.

Not bad, Dijkstra. Not bad.

If that explanation wasn't math-y enough for you, check out MIT's explanation. Same concept, just with a few more variable definitions.