We know what we have to find, so let's find it. 1. What are the intercepts? First, the x-intercepts. We need to find the roots of the quadratic polynomial. If we find them, we can celebrate by drinking a root beer. We need to find the solutions to the equation 0 = -x2 + 2x + 3
= -(x2 – 2x – 3). This equation factors as 0 = -(x – 3)(x + 1), so the solutions (and the x-intercepts) are x = 3, x = -1. We can graph these points: 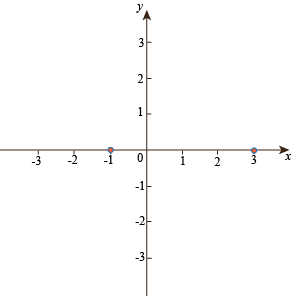
The y-intercept is the constant term, 3, so we can graph that also: 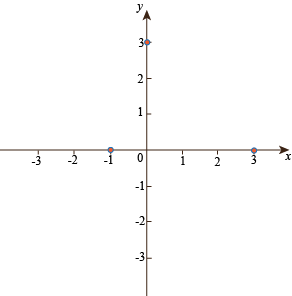
2. What is the vertex? The vertex occurs halfway between the x-intercepts -1 and 3, so at x = 1. When we plug x = 1 in to the quadratic equation, we find -(1)2 + 2(1) + 3 = 4, so the vertex occurs at (1, 4). 3. Does the parabola open upwards or downwards? Since the coefficient on the x2 term is negative, the parabola opens downwards. Putting together all the pieces, we find our graph: 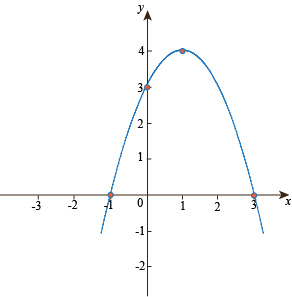
We know this graphing stuff can be infectious, but be careful. We don't want you to get a graph infection. |