Example 1
Graph the function f(x) = ex. Then add, on the same set of axes: (a) the first-degree Taylor polynomial for f(x) at 0. (b) the second-degree Taylor polynomial for f(x), centered at 0. (c) the 3rd-degree Taylor polynomial for f(x) at 0. (d) the 4th-degree Taylor polynomial for f(x) at 0. (e) the 5th-degree Taylor polynomial for f(x) at 0. |
Example 2
What is the Maclaurin series for f(x) = ex? |
Example 3
Find the MacLaurin series for f(x) = sin x. |
Example 4
Find the second-degree Taylor polynomial for |
Example 5
Find the Taylor series for the function sin x near |





 . This function curves more like ex but still gets away pretty quickly:
. This function curves more like ex but still gets away pretty quickly:
 .
If we graph the 2nd and 3rd degree polynomials with f(x) we can see that g3 sticks a little more closely to f(x) when x > 0:
.
If we graph the 2nd and 3rd degree polynomials with f(x) we can see that g3 sticks a little more closely to f(x) when x > 0:
 .
.
 . Getting even closer...
. Getting even closer...



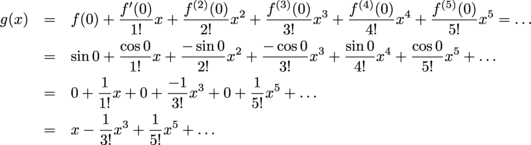



 near x = 4.
near x = 4.


 .
.

 .
. , and finally plug things into the formula.
, and finally plug things into the formula.


