Up until now, we've pretty much dealt with variations of the same area A = bh formula. We changed it to A = lw for rectangles and even A = s2 for squares, but it's essentially the same thing. How many times can you multiply two numbers together?
It's time to get freaky. No, not super freaky, but a good amount of freaky. Like having two bases—not two heads—instead of just one.
We're talking about none other than trapezoids, which are really easy to come by. As long as only two of its four sides are parallel to each other, we've got ourselves a trapezoid. They don't even have to be the same length, which means the other sides can do whatever they want, pretty much. Nothing at all like parallelograms or rectangles.
We told you. Freaky. So freaky, in fact, that we should call them Freakazoids.
They all look different, anyway. Even if we could use a single equation to calculate area for all of them, how would we start? It's like trying to go from Nebraska to the land of Oz. (Maybe that's not the best example. A detour through Kansas and we're golden.)
Let's take the characteristic that all trapezoids share: the parallel sides. We know that two parallel lines will always be the same distance apart, so let's call this distance the height. For consistency's sake, we'll use h for height…again.
We know that the two parallel sides won't have the same length because then we'd have a parallelogram. So we'll call those two sides the bases, b1 and b2. (Sometimes you'll see B and b instead of b1 and b2. They're just different ways to differentiate the two bases.) Our area formula for any trapezoid with height h and bases b1 and b2 is:
A = ½(b1 + b2)h
Thankfully, we can ignore the wonky sides that aren't parallel to each other.
Sample Problem
If the bases of a trapezoid have lengths of 4 and 5 with a height of 2, what is the area of the trapezoid?
Using the equation for the area of a trapezoid, all we have to do is plug in the lengths of the bases and the height.
A = ½(b1 + b2)h
A = ½(4 + 5) × 2
A = ½ × 9 × 2
A = 9 units2
Sample Problem
Find the height of a trapezoid that has an area of 7 units2 and bases of 7 units and 21 units in length.
We can use the same area formula for a trapezoid. This time, instead of solving for A, we can solve for the height h. Substitute 21 units for b1, 7 units for b2, and 7 units2 for A. You know the drill.
A = ½(b1 + b2)h
7 = ½(21 + 7)h
7 = ½ × 28 × h
0.5 = h
The height of the trapezoid is 0.5 units.
As freaky as trapezoids are, you probably already know that there are different types of them. Isosceles trapezoids make some attempt at being normal by making their two nonparallel sides the same length. Right trapezoids have a side that makes right angles with both bases.

Knowing these specific types of trapezoids doesn't change the formula for how to calculate area. It's still A = ½(b1 + b2)h. On the other hand, it may be useful if you don't have b1, b2, and h given to you outright.
Sample Problem
What is the area and perimeter of this trapezoid?
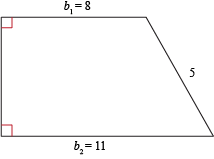
This is a right trapezoid, so we can look at it as a rectangle and a right triangle joined together. The hypotenuse of the triangle is given as 5 and we can find one of the legs by subtracting the small base from the large base, which gives us a length of 3.
We know the hypotenuse and one of the legs of a right triangle. Can you say, "Pythagorean Theorem"? We sure can. Just replace a with 3, b with h, and c with 5.
a2 + b2 = c2
32 + h2 = 52
h2 = 16
h = 4 units
The height of this trapezoid is 4 and we know that its bases are 8 and 11. Finding the area should be a breeze.
A = ½(b1 + b2)h
A = ½(8 + 11) × 4
A = ½ × 19 × 4
A = 38 units2
Well, that's all good and fine, but what about the perimeter? We know the perimeter is just all the sides added together. We already know three of the sides (the two bases ad the non-perpendicular side). Lucky for us, the height is one of the sides for a right trapezoid.
P = b1 + b2 + h + s
P = 8 + 11 + 4 + 5
P = 28 units