Gas Laws
Wacky Gaseous Behavior
Boyle's Law
Robert Boyle.
Boyle's Law, named after physicist Robert Boyle2 (that cool dude with the hair shown above), is all about the relationship between gaseous pressure and volume. Picture a certain amount of gas put into a sealed container. According to the law, if the volume of a container is increased, the pressure that the gas exerts on the walls of the container decreases. Likewise, if the volume of a container is decreased, the pressure that that gas exerts on the walls of the container increases. In order for this relationship between pressure and volume to be reliable we have to keep all other variables constant, namely temperature and the number of gas particles present.

It makes sense if you think about it. The pressure that the gas exerts on the walls of the container is caused by gas particles colliding with the wall. If we make the container that we're holding the gas in bigger (by increasing the volume) the gas particles have more room to do their thing without hitting the walls as often, which decreases the pressure. Or if we make the container smaller the gas particles will run into the walls more often, thereby increasing the pressure.
On paper, Boyle's law takes the form:
PV = k
where P is pressure, V is volume, and the value of k is a constant. Notice T (for temperature), n (for number of moles of gas), and C (for cookie) are nowhere to be seen. They don't show up in the equation because they are assumed not to change. Based on the equation for Boyle's law we can conclude with our fancy mathematical powers of deduction that pressure and volume are inversely related to each other, as one goes up the other goes down. The folks over at NASA put together a really nice animation of Boyle's Law in action. Check it out.
A typical plot of pressure versus volume for a gaseous sample can be found here. At any point on the curved line PV = k. Therefore according to Boyle's law and our fancy mathematical powers of deduction we can say that:
P1V1 = P2V2
This equation will be most useful when solving questions regarding Boyle's law.
Boyle's Law Practice Problem
A container with a movable piston (to allow volume changes) holds 500 mL of O2 at 20oC and 742 mm Hg. What will be the volume of the O2 if the pressure is increased to 795 mm Hg?Solution:
P1 = 742 mm Hg
V1 = 500 mL
T1 = 20oC + 273 = 293 K
P2 = 795 mm Hg
V2 = ?
T2 = 20oC + 273 = 293 K (note the T is held constant)
P1V1 = P2V2
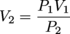
V2 = 467 mL O2
Charles' Law

Joseph Louis Gay-Lussac.
That fancy guy above is Joseph Louis Gay-Lussac, a French chemist and physicist who developed Charles' law, the relationship between temperature and volume in gases. Confused why it's called Charles' law and not Gay-Lussac's law? Gay-Lussac was an honest guy and he gave rightful credit to the unpublished work of Jacques Charles.3 You see, in 1787 Jacques Charles discovered that a bunch of different gases including oxygen, hydrogen, and carbon dioxide, all expand to the same extent when heated. He decreed that if the temperature of a gas in a container is increased, the volume of the gas increases.4 Or if the temperature of a gas in a container is decreased, the volume of the gas decreases. Just as in the case of Boyle's law, we hold the other variables (pressure and molar quantity) constant.

Let's think about this. When we increase the temperature of a gas we are increasing the kinetic energy of the particles and making them more excitable. They are moving faster and jumping around a lot more. The gas particles are also colliding with the container walls more often and with more force. As a consequence, the pressure of the gas inside the container increases. Wait a minute. Didn't we just say Charles' law declares pressure and molar volume are held constant? We did. The greater pressure in turn pushes the container walls outward, increasing the container's volume. Overall the pressure does not change, it remains constant and all is right in the world of chemistry. Check out this neat NASA animation of Charles' law in action.
Charles' law is written as:
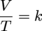
where V is volume, T is temperature, and k is a constant. Once again, pressure and number of moles are not present because they are held constant. This equation depicts a direct relationship between volume and temperature in gases. This means that as one variable increases, the second variable increases as well. Or if one variable decreases the other variable decreases, too.
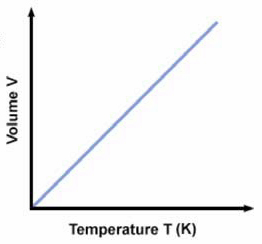
Above is a typical graph of volume versus temperature for gases. At any point on the line V/T = k. Just as we did with Boyle's law we can also say that:
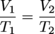
Remember to convert any temperature given in Celsius to Kelvin before solving a problem with Charles' law.
There are a lot of videos that show Charles' law in action. Watch this hot air balloon inflate. As the temperature of the gas inside the balloon is heated with a flame the balloon begins to inflate because the volume is increasing. Or check out this implosion of a metal drum. The drum is filled with a gas. When the gas is cooled the volume decreases and destroys the drum.
Charles' Law Practice Problem
A container holds 50 mL of O2 at 25ºC with a pressure of 736 mm Hg. What will be its volume if the temperature increases by 35ºC?Solution:
P1 = 736 mm Hg
V1 = 50 mL
T1 = 25ºC + 273 = 298 K
P2 = 736 mm Hg
(note the pressure is held constant)
V2 = ?
T2 = 25ºC + 35ºC + 273 = 333 K
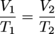
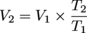
V2 ≈ 55.9 mL O2
Avogadro's Law
Avogadro's law is simple. It states: equal volumes of gases at the same pressure and temperature contain equal number of particles. Mathematically it is expressed:
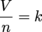
where V is volume, n is the number of particles, and k is a constant. Historically, the establishment of the relationship between volume and number of particles was a key step in understanding the connection between stoichiometry and atoms or molecules. In a nutshell, one particle of an ideal gas is mechanically no different from any other.
The Combined Gas Law
Much as the name implies the combined gas law is a combination of Boyle's law and Charles' law. It states that, for an ideal gas undergoing change from one state (with P1, V1, and T1) to a second state (with P2, V2, and T2) the following equation may be applied:
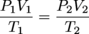
where P, V, and T mean the usual. You may have guessed n, the number of moles of gas, is assumed to be constant.
Combined Gas Law Practice Problem
The initial temperature of a 1 L sample of O2 is 20ºC. The pressure is decreased from 720 mm Hg to 360 mm Hg and the volume increases to 2.14 L. What was the change in temperature of the O2?Solution:P1 = 720 mm Hg V1 = 1 L T1 = 20 °C + 273 = 293 K
P2 = 360 mm Hg
V2 = 2.14 L
T2 = ?
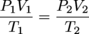
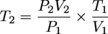
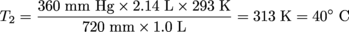
The Ideal Gas Law

Emil Clapeyron.
That fine gentleman reading the daily newspaper is Emil Clapeyron.5 He was the first to put all of the above gas laws together into one fancy form that we call the ideal gas law. Here it is in its most simplified form:
PV = nRT
The only variable we haven't discussed is R, the universal gas constant, which has a value of 0.082 atm L mol-1 K-1. Notice the pressure unit is in atm. The numerical value for R is different depending on the unit of pressure. A common mistake is to use two different units of pressure when solving ideal gas problems. If a problem gives a pressure in mmHg then either convert mmHg to atm or, if you insist, use the R value of 62.4 L mmHg mol-1 K-1.
Ideal Gas Law Practice Problem
Calculate the mass of 15 L of O2 at 27ºC and 900 mm Hg.Solution
P = 900 mm Hg
T = 27°C + 273 = 300 K
V = 15.0 L
R = 0.0821 L•atm/mol•K
PV = nRT
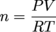

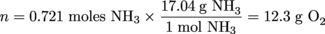
Dalton's Law of Partial Pressures
This gas law is pretty straightforward. If we have a mixture of gases in a container, according to Dalton's law, the total pressure is the sum of the pressures exerted by each of the gases in the mixture. Here's the equation that just might change your life:
Ptotal = P1 + P2 + P3 + … + Pn
where n is the total number of gases in the mixture. Each gas in a mixture creates a pressure against the container walls called a partial pressure. This pressure would be the same whether there were other gases present or not. That's why we can get the total pressure by summing all of the partial pressures.
Graham's Law

Thomas Graham.
That Graham guy sure was perceptive. He discovered that the denser a gas is, the more slowly it effuses. Effusion is the process in which individual molecules flow through a hole without colliding with another molecule. More specifically, Graham said that the rate of effusion of a gas is inversely proportional to the square root of the molecular mass of the gas molecules.6
Upon comparing the rates of effusion of two gases, Graham also said that the inverse ratio of the square roots of the masses of the two gases' molecules equals their relative rate of effusion. Say what? It makes more sense if you see the equation. Here it is:
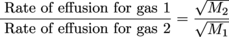
where M1 and M2 are the molecular masses of the gas particles. The molecular mass of H2 for example is 2, while the molecular mass of O2 is 32. Still confused? It will all make sense once we do a few exercises.