ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Statistics 1.1 Statistical Inference 270 Views
Share It!
Description:
AP Statistics: Statistical Inference Drill 1, Problem 1. Which of the following statements is true?
Transcript
- 00:02
Here's your shmoop du jour, brought to you by Interval Estimates.
- 00:06
Although honestly, if you're a daredevil looking to leap an interval on your bike... you're
- 00:10
going to want more than an estimate.
- 00:12
Which of the following statements is true?
- 00:15
And here are the potential answers...
Full Transcript
- 00:20
We're given four statements...
- 00:22
...and we need to find the one that ain't messing with us.
- 00:25
The first statement says that a confidence interval is a point estimate.
- 00:29
A confidence interval is an estimate of a range of values within which we would find
- 00:34
repeated sample means.
- 00:36
For example, a 90% confidence interval would mean that repeated sampling
- 00:42
would result in 90% of the sample means falling within the interval.
- 00:47
Therefore, it is not a point estimate. Rather, it is an interval estimate.
- 00:50
And Statement 1 is false.
- 00:53
Statement 2 says that a population proportion is a point estimate.
- 00:56
Again, we have to know what a population proportion is. It is the proportion of a set of data
- 01:01
that fulfills a certain criteria.
- 01:03
For example, the population proportion of people who eat fried ants at least once every
- 01:08
week out of 200 people in the population is a number we can actually calculate.
- 01:15
However, there's no estimation when we find this, so it isn't an estimate at all.
- 01:20
The first two statements are false, so we can eliminate choices A, B, and D.
- 01:25
Statement 3 says that a sample mean is a point estimate.
- 01:30
Remember that a sample mean is a single value that estimates the middle of a set of data.
- 01:35
That one value is a point. Therefore, this statement is true.
- 01:40
Finally, our last statement says that an interval estimate gives more detail about the uncertainty
- 01:43
of the estimate than a point estimate.
- 01:45
This is intuitively true, as simply seeing a mean or median
- 01:49
tells us nothing about the uncertainty of the data.
- 01:51
Whereas when we're given a confidence interval, we know a lot about how certain the data is.
- 01:57
A 99% confidence interval lets us know that 99% of sample means taken will fall within
- 02:02
the range of the interval.
- 02:03
Since both statement 3 and 4 are true, we know our answer is (E).
- 02:07
As in, "Evil Knievel's big moment."
Up Next
AP Statistics 2.1 Exploring Data. How does this change affect the mean, standard deviation, and IQR?
Related Videos
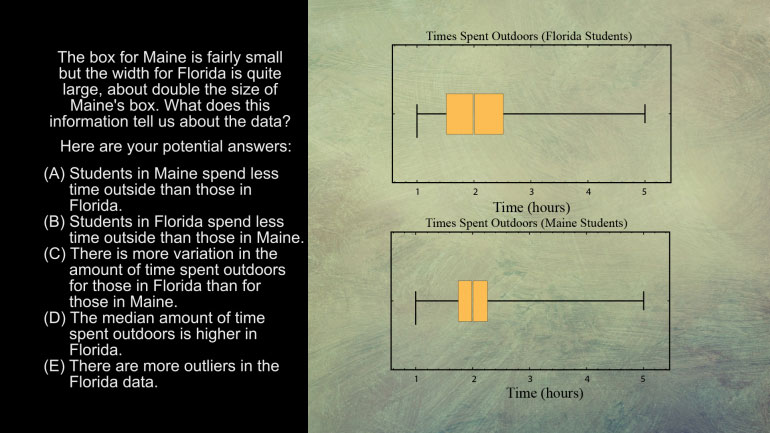
AP Statistics 5.1 Exploring Data. What does this information tell us about the data?
AP Statistics 5.2 Exploring Data. Which method would not be a good option?
AP Statistics 1.5 Statistical Inference. Which of the following statements is false?
Want to pull an Oliver Twist and ask us for more? We've gotcha covered. Head over to /video/subjects/math/test-prep/ap-statistics/ for more AP...