The Chi-Squared Test
Lies, More Lies, and… the χ2 Test
Despite the misuse and abuse they get in everyday life, when you're studying genetics, statistics really are helpful, particularly when trying to figure out if your genes are behaving in the way you think they should be. And one of the most important statistical tests you can carry out in genetics is the chi-squared (χ2) test (also known as Pearson's chi-squared test).Why would you need to carry out a χ2-test? Let's go all the way back to our yellow/green, round/wrinkled peas: from our theoretical crosses, we figured out that when you cross two heterozygous parents (RrYy), you would expect to see a phenotypic ratio of 9 round, yellow peas : 3 round, green peas : 3 wrinkled yellow peas : 1 wrinkled green pea in the offspring. But what if we actually did this cross for real? Would the numbers we were expecting to see be the same as the numbers we'd actually observe in real life? And how would you prove that what you did see wasn't down to random chance? That's where your χ2–test comes in!
Let's say we did our cross and counted the numbers of peas we actually got:
| Round Yellow Peas | Round Green Peas | Wrinkled Yellow Peas | Wrinkled Green Peas |
|---|---|---|---|
| 219 | 81 | 69 | 31 |
Because this is a test, you have to have a hypothesis that can be tested and proved either right or wrong: for the χ2–test, this is known as the null hypothesis (HO). The null hypothesis basically states that there is no difference between the results you observed and the ones you were expecting, in this case a 9:3:3:1 ratio. But how do we do that mathematically?
Here's how:
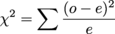
Little bit scary at first sight, isn't it? Let's break it down into its component parts so it doesn't look so bad:
First, we need to calculate the number of each phenotype we would expect to see if we did get a perfect 9:3:3:1 ratio. You do this by finding the total number of your actual peas (219 + 81 + 69 + 31 = 400) and dividing it by the numbers expected from your ratio (9 + 3 + 3 + 1 = 16). This number represents your "1" from the predicted ratio, in this case = 25. Now multiply that by 9 or 3 to get your final expected numbers, as shown in the table below:
| Phenotype | Observed (O) | Expected (E) |
|---|---|---|
| Round Yellow Peas | 219 | 225 |
| Round Green Peas | 81 | 75 |
| Wrinkled Yellow Peas | 69 | 75 |
| Wrinkled Green Peas | 31 | 25 |
| Total | 400 | 400 |
| Phenotype | Observed (O) | Expected (E) | O – E | (O – E)2 |
|---|---|---|---|---|
| Round Yellow Peas | 219 | 225 | -6 | 36 |
| Round Green Peas | 81 | 75 | 6 | 36 |
| Wrinkled Yellow Peas | 69 | 75 | -6 | 36 |
| Wrinkled Green Peas | 31 | 25 | 6 | 36 |
| Total | 400 | 400 |
| Phenotype | (O – E)2 | E | (O – E)2 / E |
|---|---|---|---|
| Round Yellow Peas | 36 | 225 | 0.16 |
| Round Green Peas | 36 | 75 | 0.48 |
| Wrinkled Yellow Peas | 36 | 75 | 0.48 |
| Wrinkled Green Peas | 36 | 25 | 1.44 |
| Total | 2.56 |
Now we need to bring in another factor, something known as the degrees of freedom (df). These take into account the number of different classes represented by the cross, in this case = 4 (as we have four different phenotypes). The more classes you have, the greater the variation you are likely to see from any expected numbers. To calculate your degrees of freedom, you take 1 from the number of classes you have, so in our example, the degrees of freedom = (4 - 1) = 3.
Nearly there! Now we have our calculated χ2 value (2.56) and our degrees of freedom (3), we can go and take a look at a χ2 probability table (there's an example of one here). We want to know if our result is statistically significant, and for most genetics tests, a significance (or confidence) level of 0.05 is used (which means that 95 times out of 100, you would see exactly what you were expecting to see, with variation occurring 5 times out of 100 purely due to random chance). If you look at the example probability table for a significance level of 0.05 (along the top) with 3 degrees of freedom (down the left hand side), the χ2 value = 7.81. Because our value is less that that (2.56), we can accept our null hypothesis and say with 95% confidence that there is no difference between the expected and observed results! If our χ2 value had been greater than 7.81, then we would have to accept that there was a statistically significant difference between the numbers we observed and the numbers we were expecting, and that yellow/green and round/wrinkled were not behaving in the way we had predicted.
Brain Snack
Karl Pearson, the man who developed the chi-squared test, really liked his numbers. He set up the first ever statistics department in London, England at University College in 1911. He was also the biographer and student of the father of eugenics, Sir Francis Galton (more about him in our History section)