First, let's start by splitting it up into pieces we can identify. The easiest to spot is the semicircle on the lower left side (going from A to B to C). The remaining pentagon (ACDEF) can be cut from A to D to form a triangle (ΔACD) and a quadrilateral (ADEF). If we add these individual areas, we'll get the area of the entire figure. Let's start by calculating the area of the semicircle, AC. Since its diameter goes from A to C, it's clear that the radius of the semicircle is 3. We can multiply the area formula for a circle by ½ to find the area of the semicircle. 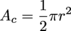
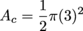
AC = 4.5π ≈ 14.1 units2 It's clear that ΔACD is a right triangle, with legs of lengths 3 – 0 = 3 and 2 – (-4) = 6. We can plug those numbers in as the base and height and find the area. AT = ½bh
AT = ½(3)(6)
AT = 9 units2 Now for that quadrilateral. Before we can do anything, let's find out what type of quadrilateral it really is. Calculating side lengths is a good way to do this. Go, go, distance formula! 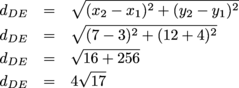
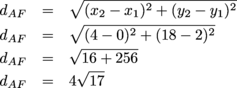
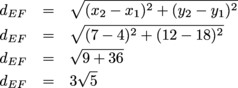
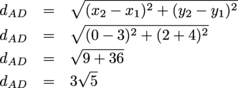
We have two pairs of congruent sides. What we have here is a parallelogram, so we know to use A = bh to find the area. Only one slight problem: what's the base and what's the height? We know that the height has to be perpendicular to the base, so let's start there. We'll set our base to DE, which has a slope of 4. Our height should have a slope of  (since negative reciprocal slopes mean perpendicular lines). (since negative reciprocal slopes mean perpendicular lines). Calculating the height of this thing might be trickier than you'd expect, so we'd suggest setting up a system of linear equations. For instance, the intersection of lines  and y = 4x – 16 will give us the point on a line perpendicular to DE that goes through (0, 2). Using the distance formula between that point, and y = 4x – 16 will give us the point on a line perpendicular to DE that goes through (0, 2). Using the distance formula between that point,  , and (0, 2) should give us the height. , and (0, 2) should give us the height. 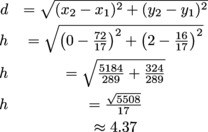
Now we can use A = bh to find the area of the parallelogram. Rather than plugging in  , we can estimate it at 16.49. , we can estimate it at 16.49. AP = bh
AP = 16.49 × 4.37
AP ≈ 72.1 units2 We're still not done. Adding the pieces together will solve the last piece of the puzzle. A = AP + AT + AC
A = 72.1 units2 + 9 units2 + 14.1 units2
A = 95.2 unis2 | 




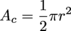
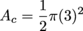
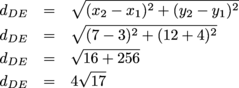
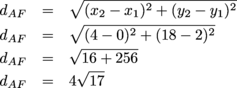
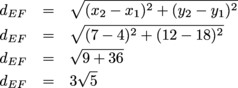
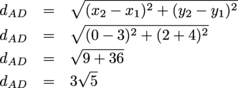
 (since negative reciprocal slopes mean perpendicular lines).
(since negative reciprocal slopes mean perpendicular lines). and y = 4x – 16 will give us the point on a line perpendicular to
and y = 4x – 16 will give us the point on a line perpendicular to  , and (0, 2) should give us the height.
, and (0, 2) should give us the height.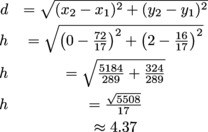
 , we can estimate it at 16.49.
, we can estimate it at 16.49.