High School: Functions
High School: Functions
Trigonometric Functions HSF-TF.B.7
7. Use inverse functions to solve trigonometric equations that arise in modeling contexts; evaluate the solutions using technology, and interpret them in terms of the context.
Students should know that just because trigonometric functions are involved in modeling doesn't mean they pose in Prada and Armani apparel. Well, not since Secant tripped down the runway of the 2007 Fashion Extravaganza in Milan. Darn those 12-inch stilettos.
Trigonometric functions dabble in other kinds of modeling. We're talking about triangles, harmonic oscillators, and other realms of geometry and even physics. Maybe not as glamorous, but still very important.
Students should be able to apply trig functions and their inverses to particular situations. In most cases, this means finding side lengths, angles, and trig ratios of right triangles. Sometimes, our angle will be θ. Other times it will be 2θ. But what if it's θ2 + 3θ – 40? This involves applying the trig functions and using them algebraically.
Since trigonometric equations can be intimidating, working a trigonometric equation and a regular algebra equation side by side while comparing steps may help. Students will see that just like they solve for x in a regular algebraic equation, they solve for θ in a trigonometric equation.
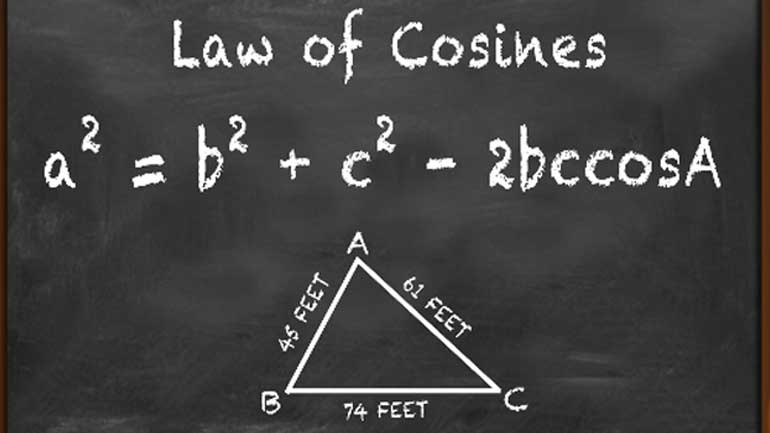
Once students are comfortable with right triangles, they can take trig functions a step further. We can apply these functions in order to solve triangles that are not right triangles using the Law of Sines and the Law of Cosines.
We can use trigonometric functions and their inverses to estimate elevations, evaluate distances across bodies of water, determine angles for vehicles, calculate wavelengths of light, and even model our very sleep cycles. Obviously, they're useful for more than finding the perfect angle for tilting a Louis Vuitton fedora. (It's 19.4°, in case you're wondering.)
Here's a recap video on the Law of Sines.
As well as a recap on the Law of Cosines