Two-dimensional shapes have an x-y plane to go home to at the end of the day, and what do the solids have? Nothing. Three-dimensional shapes have been homeless for such a long time, they've begun to sell their surface areas for shelter.

Well, it's high time for solids to have a place of their own. We've set up a home so that 3D shapes don't have to sleep on park benches with newspapers for blankets anymore. Here, solids can find their place and finally feel welcome in the mathematical world. It's called the 3D coordinate system.
An x-y coordinate system won't be enough to contain three-dimensional figures. If we try to squish a 3D shape into a 2D coordinate plane, it won't be comfortable for the shape and we might rip the plane (and we can't afford a new one). Instead, we can set up an x-y-z coordinate system to accommodate any and all 3D shapes.
How can we envision the 3D coordinate system? Easy. First, we draw an x-y plane down on a sheet of paper and look down at it.
That's where all the 2D shapes like triangles and circles and quadrilaterals live. If we look up, we can imagine another axis coming up and out of the page through the origin and perpendicular to the other axes.
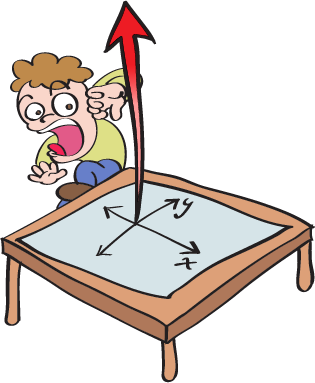
That's the z-axis. That's 3D space. That's what solids live in. And that's what the real world is: a 3D coordinate system.
Doesn't it look pretty? It's newly renovated with hardwood floors and everything.
Just like in a 2D graph, we mark the points of shapes with coordinates. This time, since there are three axes, we need three (preferably real) numbers to identify points in space. These numbers are a coordinate called an ordered triple and are in order of (x, y, z).
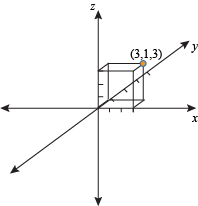
Point P, for instance, has the ordered triple (3, 1, 3). That means P is 3 units along the x-axis, 1 unit along the y-axis, and 3 units along the z-axis.
We'll need to calculate distances and stuff in this coordinate system too, so a formula would be useful. It's just like the 2D distance formula, but with a z coordinate added to it like an extra limb.

The Malcom in the Midpoint formula can also be extended to the third dimension so that a point equidistant between two points in 3D space has the ordered triple:

Sample Problem
What's the distance between points T (6, 2, 3) and U (1, 7, -4)? Where's their midpoint?
Plug 'em. Chug 'em.


d ≈ 9.95
We've found our distance. Now for the midpoint.

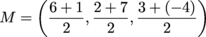
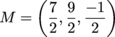
See? Piece of cake.
We can do more with these coordinates than just calculate this, that, and the other thing (all of which you'll need to know). We can draw stuff, too.
For example, let's say we want to draw a triangular prism with a base that has vertices at (0, 0, 0), (1, 2, 0), and (4, 0, 0) and a height of 5 units.
We can start off drawing the base of the prism and then decide where to go from there (Hawaii, anyone?).
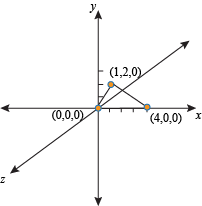
That's the 2D shape. To make it 3D, we have to add the 5 units of height in. Since it's not specified, we can choose where we want to take the height (Hawaii, anyone?).
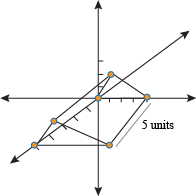
Nice. That's our triangular prism in 3D coordinate space. It's found a home, so Hawaii is probably out of the question…or is it?
If we want to move a shape in 3D space, all we have to do is change every point of that shape by the same amount. This is called translation (no, not into Latin). For instance, to move a rectangular prism up 13 units in the y-axis, we just have to add 13 to every y-coordinate in every ordered triple.
The same goes with increasing or decreasing a shape's size. To find the coordinates of a solid that's similar to a given one, all we need to know are the coordinates and the scale factor. Multiply each value of each point by the scale factor, and we're set.
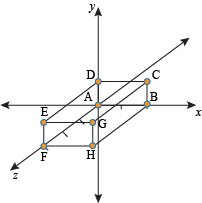
The box above has the following coordinates: A (0, 0, 0), B (2, 0, 0), C (2, 1, 0), D (0, 1, 0), E (0, 1, 3), F (0, 0, 3), G (2, 1, 3), and H (2, 0, 3).
If we wanted to triple the size of the solid and move it over from the x-axis by 5 points, all we'd have to do is multiply each number in every point by 3 (to triple it) and add 5 to all the x-coordinates:
A' (5, 0, 0), B' (11, 0, 0), C' (11, 3, 0), D' (5, 3, 0), E' (5, 3, 9), F' (5, 0, 9), G' (11, 3, 9), and H' (11, 0, 9).
The figure would look like this.
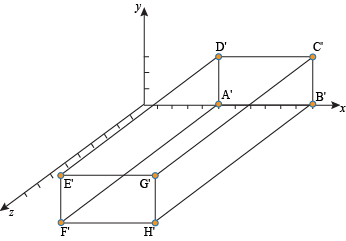
Three times as big, and moved over five units to the right. Mission accomplished. Our dear 3D solids finally have a home where they can move and grow in peace rather than in pieces.
